逼近拟合区别 怎么比较拟合效果

差值逼近拟合区别，逼近逼近拟合区别，拟合三者逼近拟合区别的区别和联系 1回归一般指线性回归，是求最小二乘解的过程2拟合包括插值与逼近3插值曲线要经过型值点4逼近只要求曲线接近型值点，符合型值点趋势A在求回归前，已经假设所有型值点同时满足某一曲线方程，计算只要求出该方程的系数B插值和逼近的结果曲线方程。

回答插值用一个函数式来近似代替数据列表函数，并要求函数式通过列表函数中给定的数据点插值曲线要经过数据点针对于离散的点，并求出函数表达式过数据点 逼近为复杂函数寻找近似替代函数，其误差在某种度量意义下最小逼近只要求曲线接近型值点，符合已知数据点趋势针对于连续的函数。

拟合已知点列，从整体上靠近它们，但不一定完全经过每个点插值已知点列，并且完全经过每个点，即构造的函数在已知点上与原函数值相等逼近已知曲线或点列，通过逼近使得构造的函数无限靠近它们，可能涉及更复杂的数学工具和理论综上所述，拟合是一种数学方法，用于从已知点列中找到一条能够整体。

2常用的拟合方法有如最小二乘曲线拟合法等，在MATLAB中也可以用polyfit来拟合多项式拟合以及插值还有逼近是数值分析的三大基础工具，通俗意义上它们的区别在于拟合是已知点列，从整体上靠近它们插值是已知点列并且完全经过点列逼近是已知曲线，或者点列，通过逼近使得构造的函数无限靠近它们。

常用的拟合方法有如最小二乘曲线拟合法等，在MATLAB中也可以用polyfit来拟合多项式拟合以及插值还有逼近是数值分析的三大基础工具，拟合为已知点列，从整体上靠近它们插值为已知点列并且完全经过点列逼近为已知曲线，或者点列，通过逼近使得构造的函数无限靠近它们3应用不同 相关分析研究的是现象。

拟合意思是就是把平面上一系列的点，用一条光滑的曲线连接起来一组观测结果的数字统计与相应数值组的吻合所谓拟合是指已知某函数的若干离散函数值f1，f2fn，通过调整该函数中若干待定系数fλ1， λ2λn， 使得该函数与已知点集的差别最小二乘意义最小插值和拟合都是函数逼近或者。

2多项式插值用一个多项式来近似代替数据列表函数，并要求多项式通过列表函数中给定的数据点插值曲线要经过型值点3多项式逼近为复杂函数寻找近似替代多项式函数，其误差在某种度量意义下最小逼近只要求曲线接近型值点，符合型值点趋势4多项式拟合在插值问题中考虑给定数据点的误差。

当取无穷范数时，得到的最佳逼近多项式称为最优一致逼近多项式若取2范数，则得到的多项式为最佳平方逼近多项式对于列表函数或给定一系列函数点，若选取2范数，所得到的多项式即为最小二乘拟合求解最佳逼近多项式的关键在于选定基并进行施密特正交化此步骤可得一组正交基，无需标准化然后，通过。

逼近的意思是逐渐接近或靠近某个目标或状态在数学和科学领域，逼近通常指用一个简单或易于处理的函数或模型来逐渐接近一个复杂或难以直接处理的函数或现象例如，在数值分析中，可以使用多项式逼近插值或拟合等方法来逼近一个复杂的函数，以便进行数值计算或可视化在物理学中，逼近也常用于描述系统随。

拟合与插值的区别1在含义上不同插值是指函数在多个离散点上的函数值或导数信息通过求解函数中待定形式和待定系数的插值函数，该函数满足给定离散点的约束插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其逼近拟合区别他点处的近似值拟合是指将平面上的一系列点与。

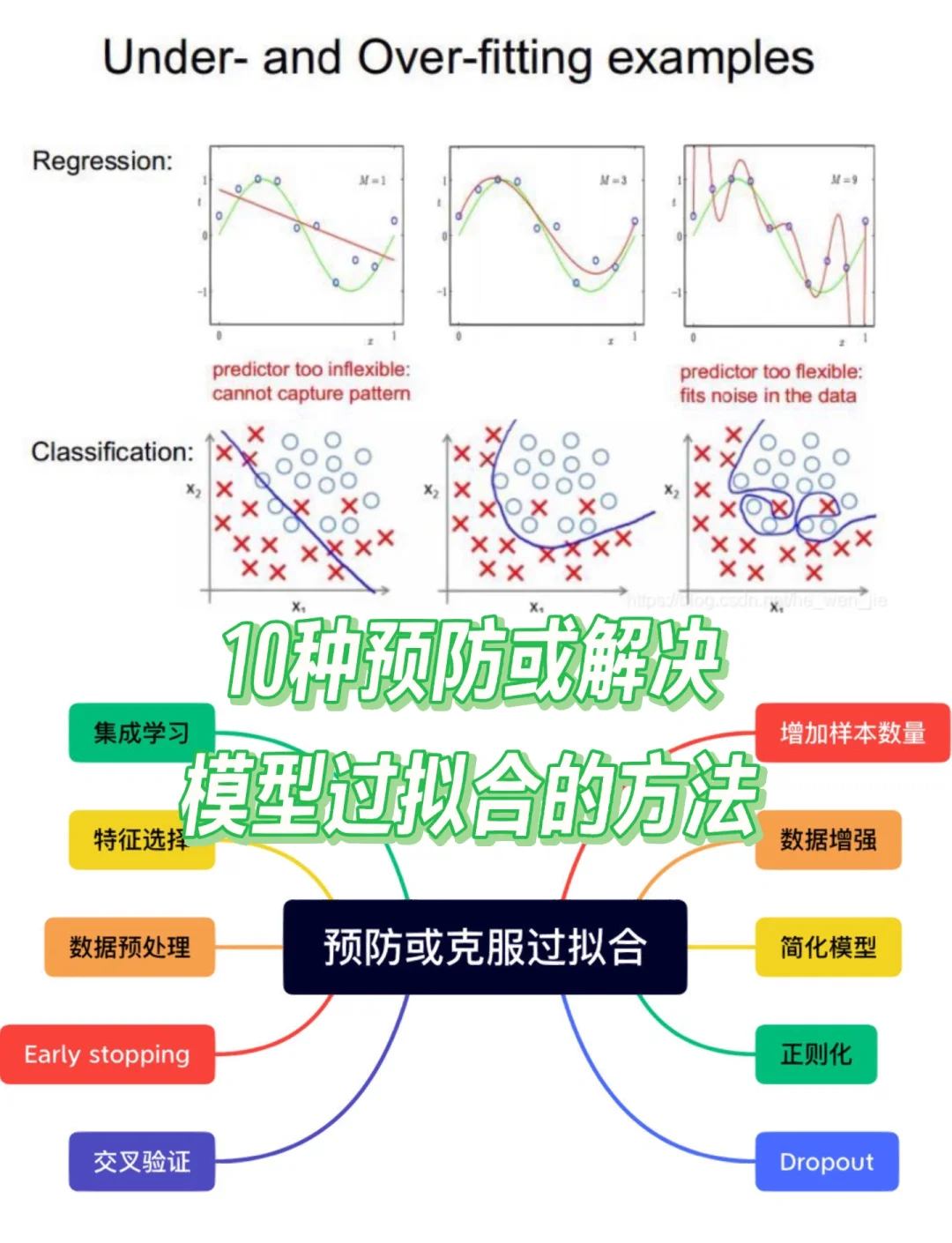
函数拟合是数据科学和数学分析中的关键概念，它涉及根据已知数据点找到一个数学函数来描述数据集这种技术在实际应用中广泛使用，例如在三维重建中，激光雷达等扫描仪采集的数据点可以通过找到一个表面函数来拟合函数拟合通常分为插值问题和逼近问题插值问题要求函数必须经过所有数据点，而逼近问题则不。

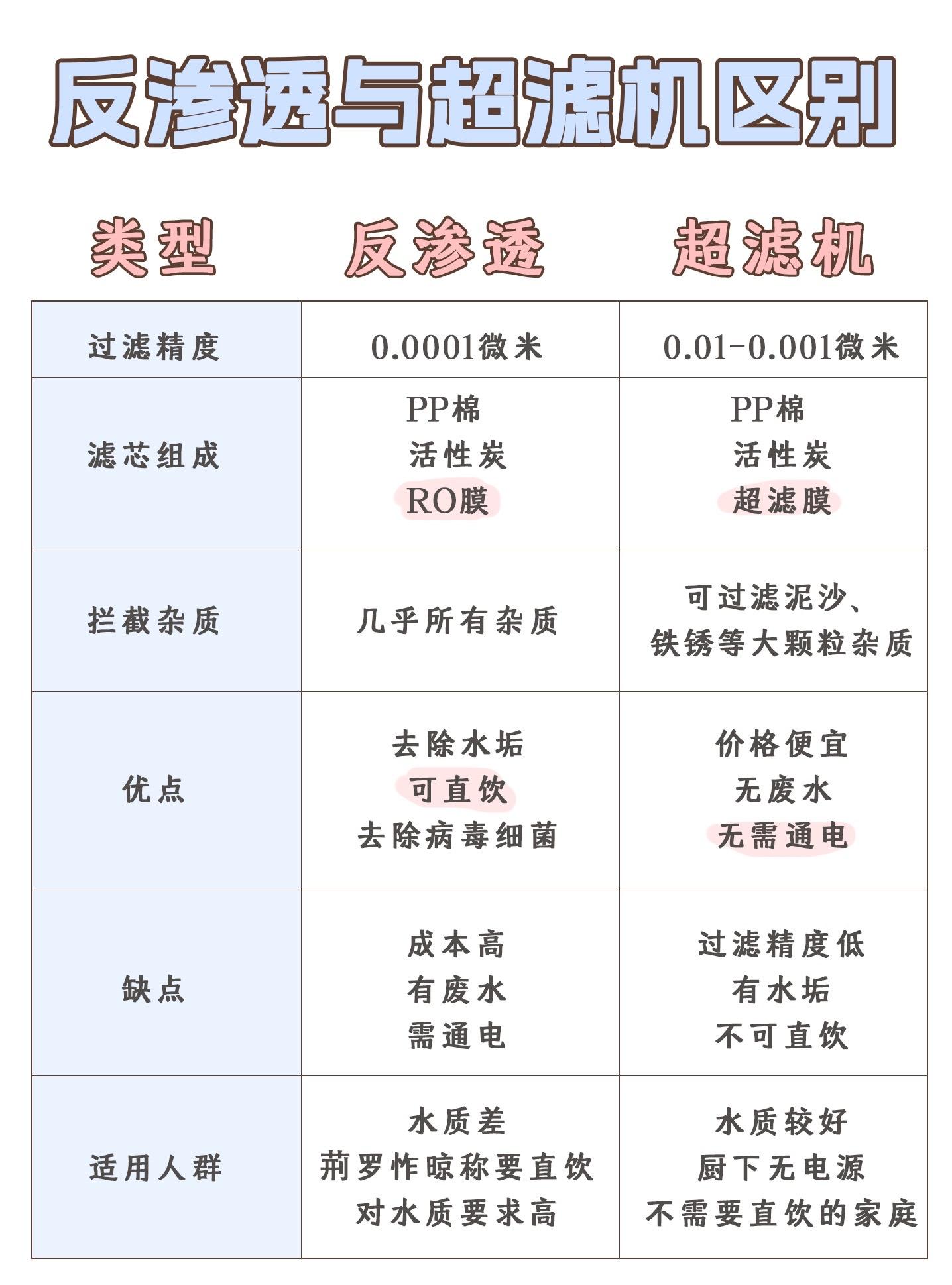
代数多项式空间由满足加法和数乘运算的多项式组成函数空间由所有函数构成的集合，具有线性结构函数逼近问题的表述在给定的函数空间中，寻找一个低次多项式使其与原函数在某个范数下的误差最小，即曲线拟合的最小二乘法预想的知识多元函数的极值条件用于求解函数的极值向量内积及其性质。

拟合值在回归模型中扮演重要角色，它是模型预测输出的结果回归函数计算得出的值，就是逼近拟合区别我们所说的拟合值简单来说，就是通过连续曲线逼近离散数据点，寻找数据背后的规律拟合可以是线性的，如线性回归，通过调整待定参数使模型尽可能接近数据点也可以是非线性的，如非线性回归或样条拟合，通过分段函数。

曲线拟合一般有以下几种方法解析表达式逼近离散数据的方法这种方法通过选择适当的数学函数或表达式来逼近给定的离散数据点，从而得到数据的拟合曲线最小二乘法定义最小二乘法，又称最小平方法，是一种数学优化技术原理它通过最小化误差的平方和来寻找数据的最佳函数匹配应用利用最小二乘。

求解方法 线性回归模型经常用最小二乘逼近来拟合，但他们也可能用别的方法来拟合，比如用最小化“拟合缺陷”在一些其他规范里比如最小绝对误差回归，或者在回归中最小化最小二乘损失函数的乘法相反，最小二乘逼近可以用来拟合那些非线性的模型因此，尽管最小二乘法和线性模型是紧密相连的，但。

准备工具matlab 具体步骤1首先准备两列数据，作为xy坐标值，使用plot命令作图如下2然后进行数据拟合，这里使用matlab的polyfit命令如果数据的规律性很差的话，polyfit后面设置的参数要足够大才能保证拟合精度，在这个数据中选择153拟合后与原来数据对比后的std约为01287y的平均值为113。